Super-Masks: Are They Good Initializations?
A large advancement in understanding neural networks was the discovery of lottery tickets. Subgraphs of initializations that are correlated to better positioning in the loss manifold can be discovered through pruning of a trained network. This was investigated after a plethora of empirical pruning results, that on mulitple state-of-the-art models parameters can be reduced up to 90% with minimal reduction to accuracy. Investigating this further, some cool people at Uber discovered Super-Masks. Super-Masks are parameter masks that find a subgraph of the models initialization that performs relatively well. This means with no actual change to the initialization weights themselves, there exists a suitable model within. How AMAZING is that???
So how do we solve for this mask
One question the supermask paper left me with is, how good is it as an initialization? Lottery tickets show quicker training with slightly stronger performance than the original. Does this still hold up? So lets do some preliminary experimentation. I look into mnist and cifar10, specifically using Wide Resnet 28. I modify the implementation from keras-contrib to allow for learned masking of the convolution and dense layers. For experiments, I use a batch size of 128 and a learning rate of .01 for training both the mask-only and weight-only setups for 30 epochs. Also for all training sessions we use random flips, translations and rotations for data augmentation. I then also take the best masked version, freeze the mask, unfreeze the weights and train up to 30 epochs as well. Note that for when I fine tune the supermasked model I use a reduce learning rate of 1e-5 because in practice ive noticed empricially the supermask to be extremely close to the local minimum, and any larger sized jumps almost entirely wiped out the boost of utilizing the super mask.
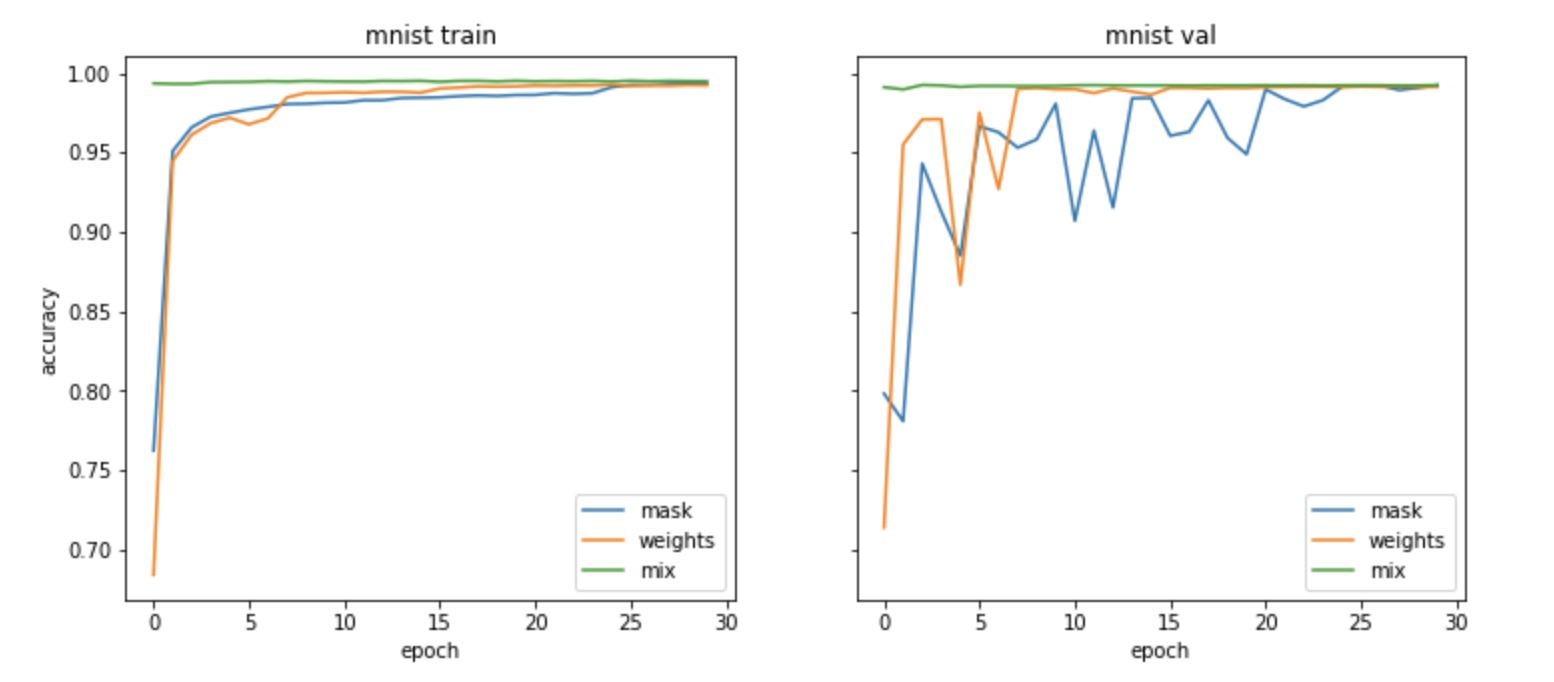
MNIST Training
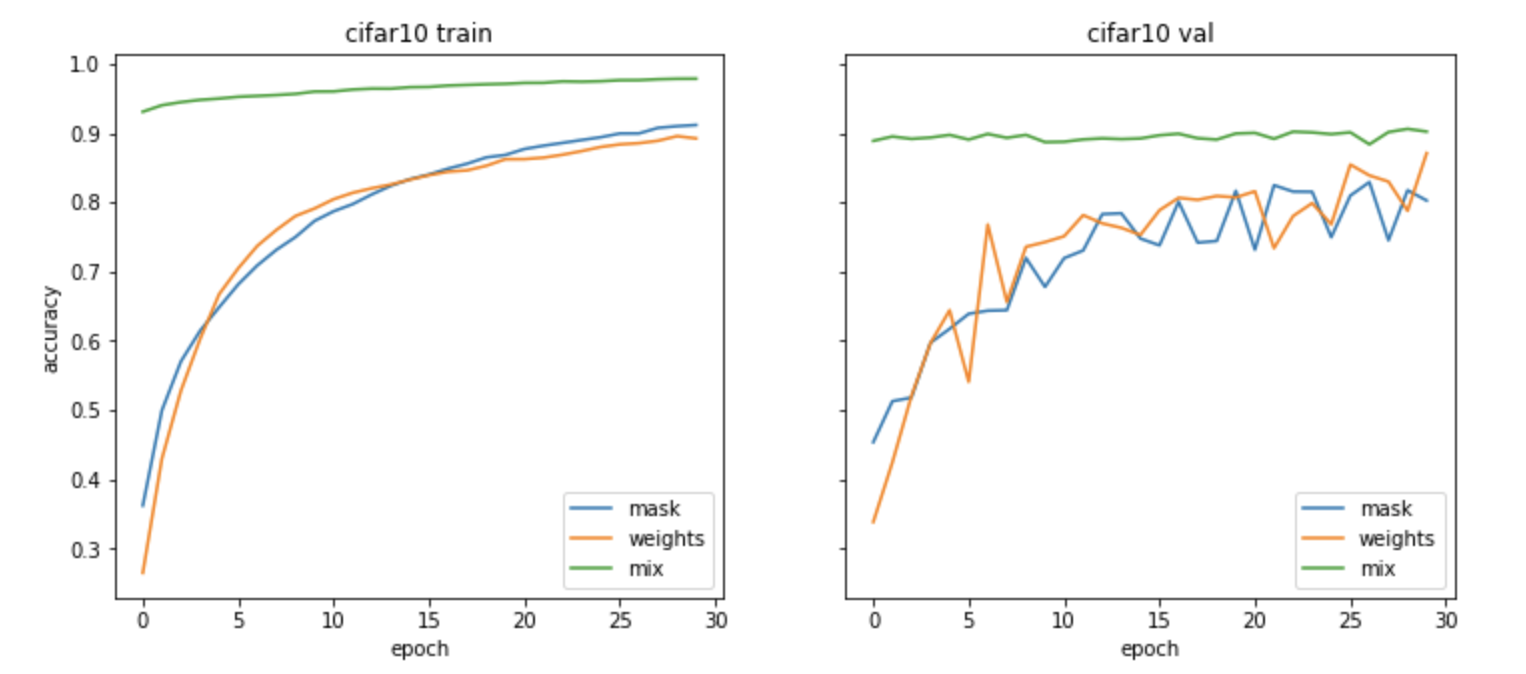
Cifar10 Training
As you can see in the above two figures, mnist supermasks achieve similar results with equal training times as the normal regime. In this case, I do not see much improvement from using it as an initialization, but this is probably because they all converge to similar minima quickly. Cifar10 on the other hand, we see equal training from both schemes for most of the way but then using the masked variation as an initialization we see a large jump in accuracy. This is really interesting to see. In the initial paper, on Cifar 10 they showed good results, but they did not do as well as the conv nets (except for the small model used for mnist), but here on a deep competetive model, we actually see sheer masking can do wonders. Moreso, starting from the masked initialization leads to a decent boost (the green lines in the cifar10 training figure). So lets see what else we can learn from these experiments.
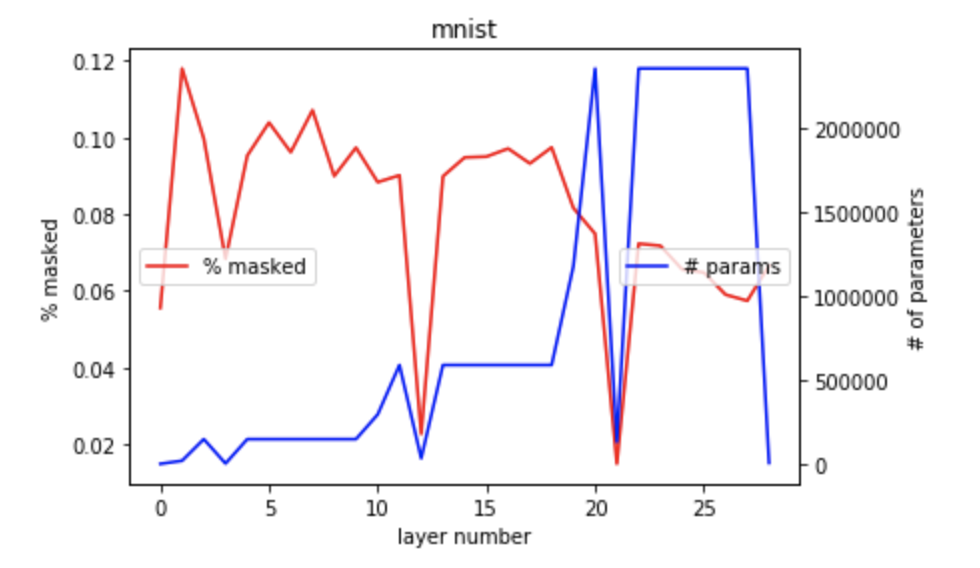
MNIST mask utilization
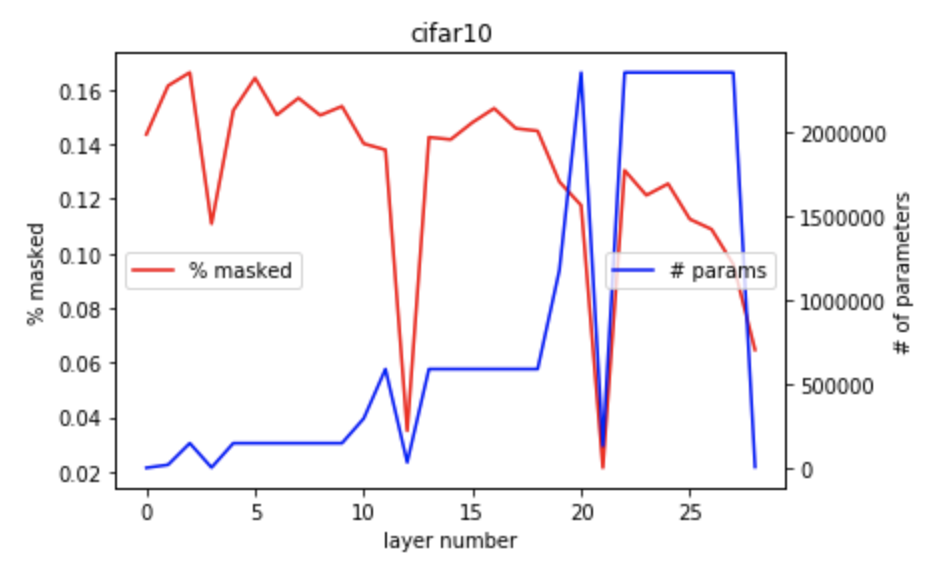
Cifar10 mask utilization
In the above two figures, we see a very specific pattern: if layers had less weights, the mask percent dropped heavily. I explain this with the obvious consideration of 'less weights / filters = information bottleneck = much harder to mess with'. I do want to note that no layer masks more than ~16%, so unlike these tiny lottery tickets discovered by pruning a trained model, were seeing Dense masks on random initializations that perform amazingly both by themselves and as initializations. A good addition in the future would be to invesitgate this discrepancy between lottery tickets and these super-masks because they do seems to be working on different properties of neural networks and their loss manifold.
The goal of this post was to describe and play with SuperMasks and answer if Super-Masks work as stronger initializations? From the experiments I did, I show you can achieve a boost in performance using this strategy! Note I did only do a small subset of experiments on small datsets, so seeing if this extends to larger datasets would be a fun continuation too.
I hope you guys enjoyed the post and here is the repo for reproduction and playing yourself with the Super-Masks
